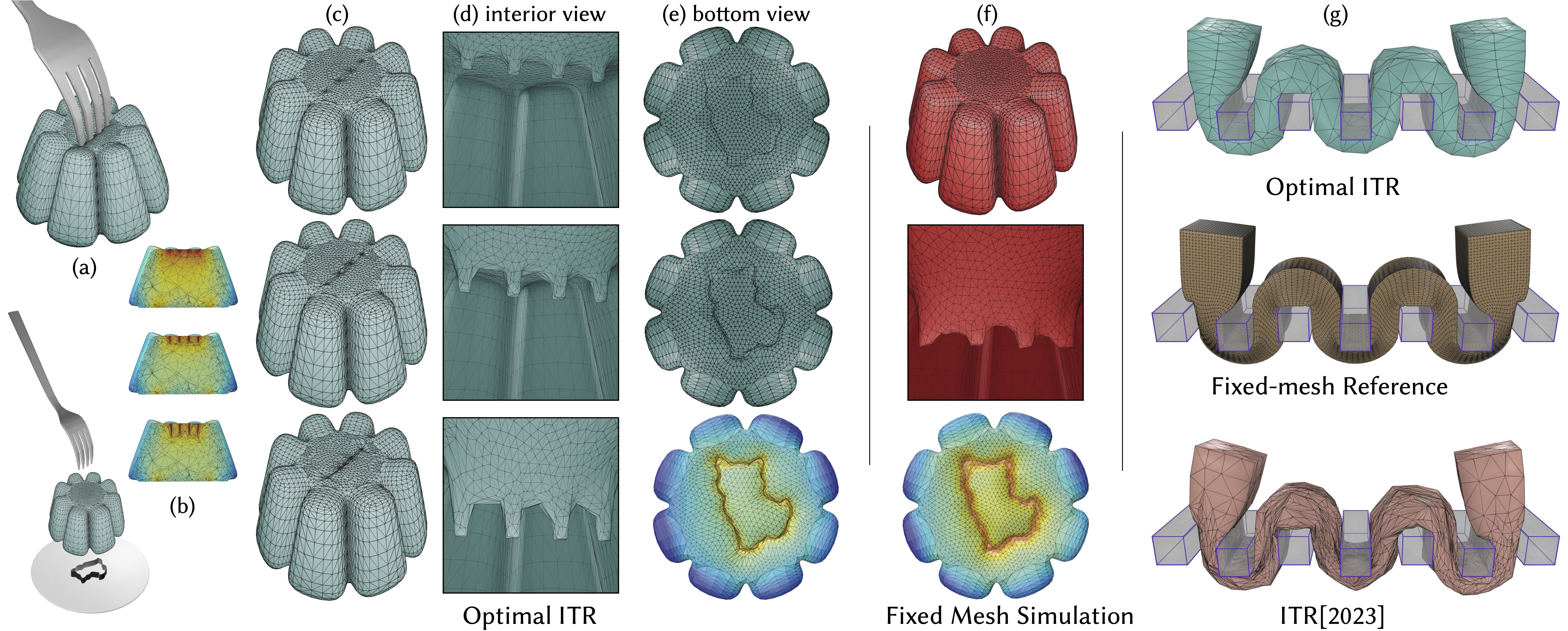
We propose a coupled mesh-adaptation model and physical simulation algorithm to jointly generate, per timestep, optimal adaptive remeshings and implicit solutions for the simulation of frictionally contacting elastodynamics. To do so, we begin with Ferguson et al.'s [2023] recently developed in-timestep remeshing (ITR) framework, which proposes an Incremental Potential based objective for mesh refinement, and a corresponding, locally greedy remeshing algorithm to minimize it. While this initial ITR framework demonstrates significant improvements, its greedy remeshing does not generate optimal meshes, and so does not converge to improving physical solutions with increasing mesh resolution. In practice, due to lack of optimality, the original ITR framework can and will find mesh and state solutions with unnecessarily low-quality geometries and corresponding physical solution artifacts. At the same time, we also identify additional fundamental challenges to adaptive simulation in terms of both ITR's original remeshing objective and its corresponding optimization problem formulation.

In order to extend the ITR framework to high-quality, optimal in-timestep remeshing, we first construct a new remeshing objective function built from simple, yet critical, updates to the Incremental Potential energy, and a corresponding constrained model problem, whose minimizers provide locally optimal remeshings for physical problems. We then propose a new in-timestep remeshing optimization that jointly solves, per-timestep, for a new locally optimal remeshing and the next physical state defined upon it.

To evaluate and demonstrate our extension of the ITR framework, we apply it to the optimal r-adaptive ITR simulation of frictionally contacting elasto-dynamics and statics. To enable r-adaptivity we additionally propose a new numerical method to robustly compute derivatives of the L2-projection operator necessary for optimal mesh-to-mesh state mappings within solves, a constraint model to enable on-boundary node adaptivity, and an efficient Newton-type optimization method for practically solving each per-timestep r-adaptive ITR solution. We extensively evaluate our method on challenging large-deformation and frictionally contacting scenarios. Here we observe optimal r-adaptivity captures comparable and better accuracy than unadapted meshes orders-of-magnitude larger, with corresponding significant advantages in both computation speedup and decrease in memory usage.